Experiment 13
Introduction
In Experiments #10 and #12 we observed photons acting like particles. In Experiment #11 a photon’s actions could only be explained using wave-like behavior. In 1978, John Wheeler proposed an experiment to test the limits this paradox. He designed the experiment to answer the following questions:
- Does the photon decide to travel as a wave or a particle depending on the experimental setup?
- And if yes, when does the photon decide?
Experiment #13
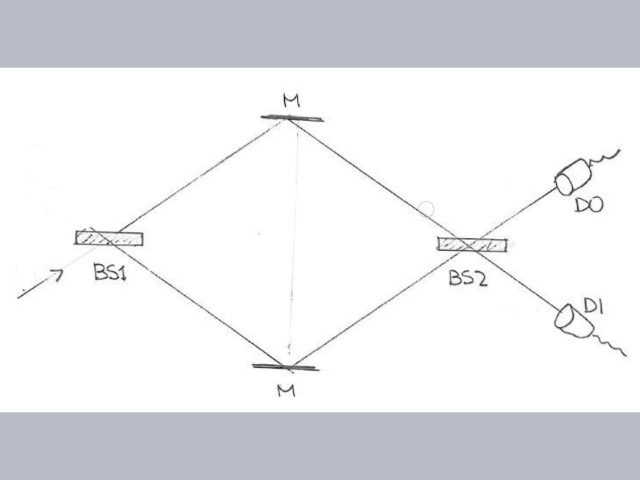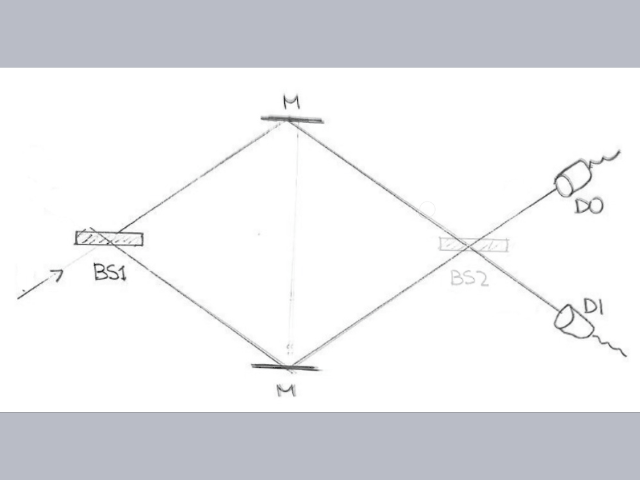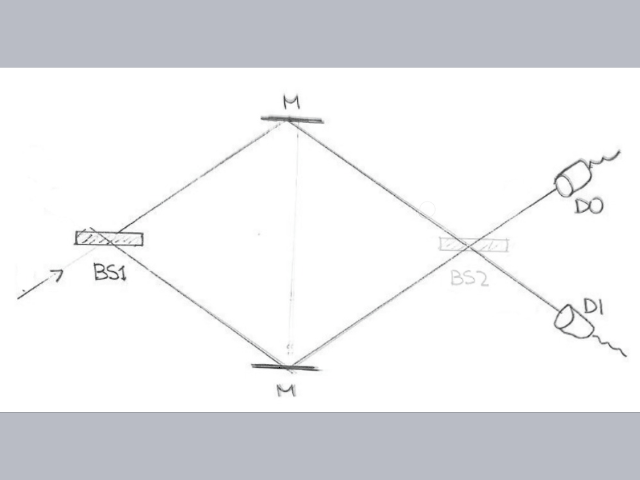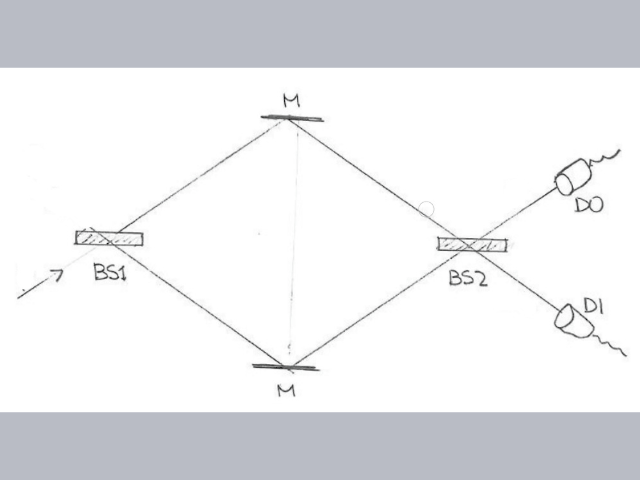
Combine the setups from Experiment #11 and #12 by randomly inserting the second beamsplitter AFTER the photon has interacted with the first beam splitter. This allows the photon to take one of six paths:
| State name | Path at BS1 | BS2 present | Path at BS2 | Detector | Probability |
|---|---|---|---|---|---|
| RX | Reflected | No | N/A | D1 | ? |
| TX | Transmitted | No | N/A | D0 | ? |
| RR | Reflected | Yes | Reflected | D1 | ? |
| RT | Reflected | Yes | Transmitted | D0 | ? |
| TR | Transmitted | Yes | Reflected | D0 | ? |
| TT | Transmitted | Yes | Transmitted | D1 | ? |
We have seen both of the setups independently, but now the decision to add the second beamsplitter takes place during the experiment.
Results
Let’s examine two of the Smalltalk simulation runs. In the first example, the second beamsplitter was omitted from the setup.
Emitting a photon from lower path. >> #(0 1)
Photon passing through a beam splitter. >> #(0.4999999999999999 0.4999999999999999)
Second beamsplitter omitted from setup.
Photon bouncing off of a mirror. >> #(0.4999999999999999 0.4999999999999999)
Photon finally detected with following probabilities: >> #(0.4999999999999999 0.4999999999999999)
We observe detection probabilities similar to those in Experiment #12. In the next example:
Emitting a photon from lower path. >> #(0 1)
Photon passing through a beam splitter. >> #(0.4999999999999999 0.4999999999999999)
Second beamsplitter inserted into setup after mirror.
Photon bouncing off of a mirror. >> #(0.4999999999999999 0.4999999999999999)
Photon passing through a beam splitter. >> #(0.9999999999999996 0.0 )
Photon finally detected with following probabilities: >> #(0.9999999999999996 0.0)
We observe detection probabilities similar to those in Experiment #11. Filling in the results chart we notice that the table reads as if there were two different experiments going on (i.e. the total observation probability adds up to 2.0!)
| State name | Path at BS1 | BS2 present | Path at BS2 | Detector | Probability |
|---|---|---|---|---|---|
| RX | Reflected | No | N/A | D1 | 0.50 |
| TX | Transmitted | No | N/A | D0 | 0.50 |
| RR/TT | ? | Yes | ? | D1 | 0.0 |
| RT/TR | ? | Yes | ? | D0 | 1.0 |
This is because there are two experiments happening - as soon as you insert the second beamsplitter you change the experiment.
Interpretation
It is clear that the behavior of the photon in the interferometer depends on the choice of second beamsplitter, even when that choice is made after the photon enters the interferometer. In Wheeler’s words,
“we have a strange inversion of the normal order of time. We, now, by moving the mirror in or out have an unavoidable effect on what we have a right to say about the already past history of that photon”
It may be tempting to interpret this experiment as a case of retrocausality, whereby the insertion of the second beamsplitter causes the photon to retroactively act like a wave instead of a particle. However, this is a leap too far.
Experiment #13, also known as the delayed-choice experiment, demonstrates a subtle point of wave-particle duality - a photon’s behavior is always governed by the Schrödinger equation, yet when measured, it is observed as a particle whose location is determined by the Born rule.
This is what is meant by a photon acting like a wave and a particle. But what about Experiments #10 and #12, where the photon acted only like a particle and not like a wave? WRONG. The photon was both, but the wavefunction predicted behavior that did not have any interference (i.e. it is particle-like).
Summary
Experiment #13 presented John Wheeler’s delayed-choice experiment. An interesting variation of this experiment is called the delayed-choice quantum eraser.
Appendix: The Smalltalk code
The full Pharo package can be found at dlfeps/MZI.